معادلات تفاضلية
| معادلات تفاضلية |
|---|
 |
| Classification |
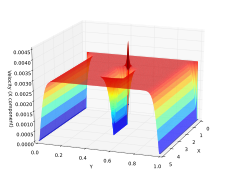
| الحل |
في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقاتها هذه المعادلات . تبرز المعادلات التفاضلية بشكل كبير في تطبيقات الفيزياء و الكيمياء ، وحتى النماذج الرياضية المتعلقة بالعمليات الحيوية و الإجتماعية و الإقتصادية .
يمكن تقسيم المعادلات التفاضلية إلى قسمين :
- معادلات تفاضلية نظامية تحتوي على توابع ذات متغير مستقل واحد و مشتقات هذا المتغير .
- معادلات تفاضلية جزئية تحتوي دوال رياضية لأكثر من متغير مستقل مع مشتقاتها الجزئية .
تعرف رتبة المعادلة التفاضلية على أنها أعلى رتبة لمشتق موجود في هذه المعادلة : فإذا حوت المعادلة مشتق أول و مشتق ثان فقط تعتبر من الرتبة الثانية ... وهكذا .
المعادلات التفاضلية من الرتبة الأولي تحتوي على مشتقات أولى فقط .
طرق حل المعادلات التفاضلية
توجد طرق عديدة لحل المعادلات التفاضلية منها.
- طرق تحليلية Analytic Solution
- طرق رقمية Numerical Solution
ويوجد أكثر من أسلوب للحل العددي وكذلك التحليلي
كما توجد معادلات مشهورة مثل معادلات لابلاس وبرنولي وغيرهم
راجع ما يلي :
[ http://www.physics.orst.edu/~rubin/nacphy/ComPhys/DIFFEQ/EXT/class/class.html معادلات تفاضلية]